How do I apply rotational base fixity to a column?
Rotational base fixity can be assigned to the support under a column via the Properties window.
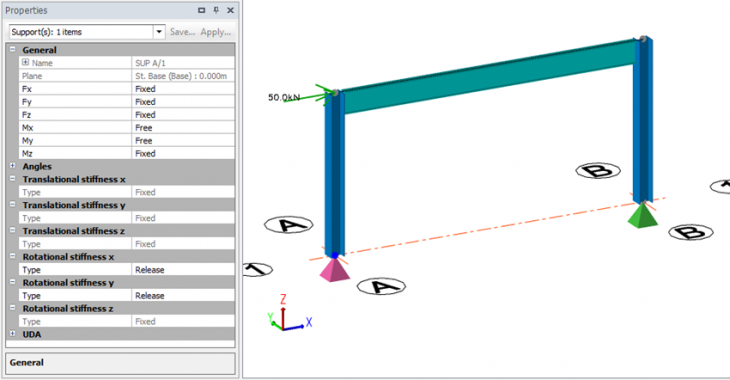
For the selected support the translational and rotational degrees of freedom can be assigned. These can be Fixed or Free. If Free then a stiffness can be assigned as either Release, Spring Linear, Spring Non-linear, Nominally Pinned or Nominally Fixed.
Before we assign a stiffness, however, it is crucial that we understand the local coordinate system for the column and support. This page provides an explanation for the special case for 1D members and a general case for 1D members. We will elaborate on the axis system in this article so everything is in one place.
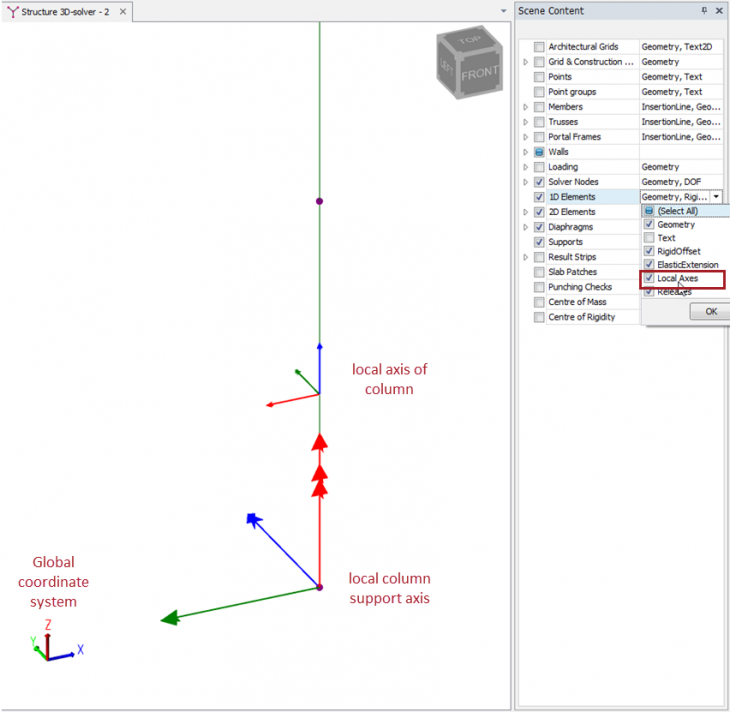
If we switch to a Solver view regime we can see the Global axis, local column axis and the local support axis system to gain an understanding.

Common to all systems is the color coding. Where X is blue, Green is Y and Red is Z.
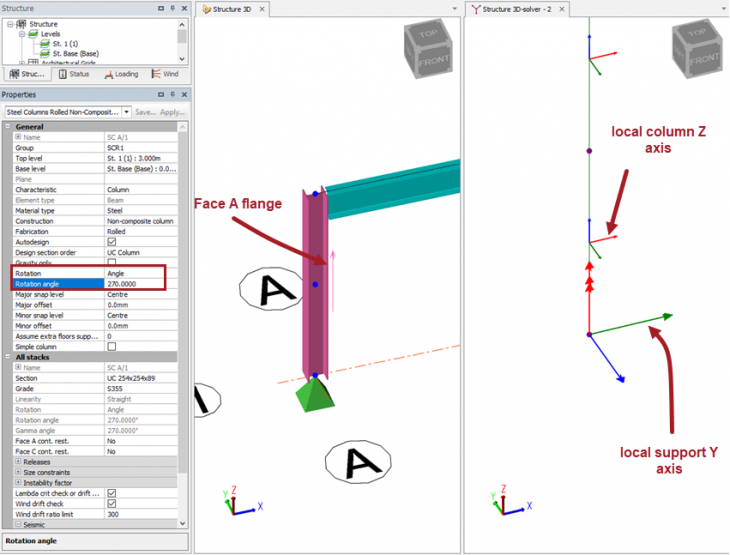
We should also add that a column has a Face A and a Face C flange (this is similar to a beam which has a top and bottom flange). The column Rotation angle input determines the orientation of the column (default is zero) and hence we need to know which flange is Face A and which is Face C. The local column Z axis always points towards the Face A flange. Turning on Scene Content > Member > Direction will show an arrow on Face A of the column. (See this article here). This is important when defining restraints to the columns. Perhaps in your models you may consider always aligning the columns so that Face A is always positioned to the outside of a building?
The screenshots below show how a change in the rotation angle of the column determines both the local axis system of the column and the underlying support axis system. The support angle is locked to the orientation of the column so the support axis moves with the change in the column orientation.
Rotation of column 0 deg
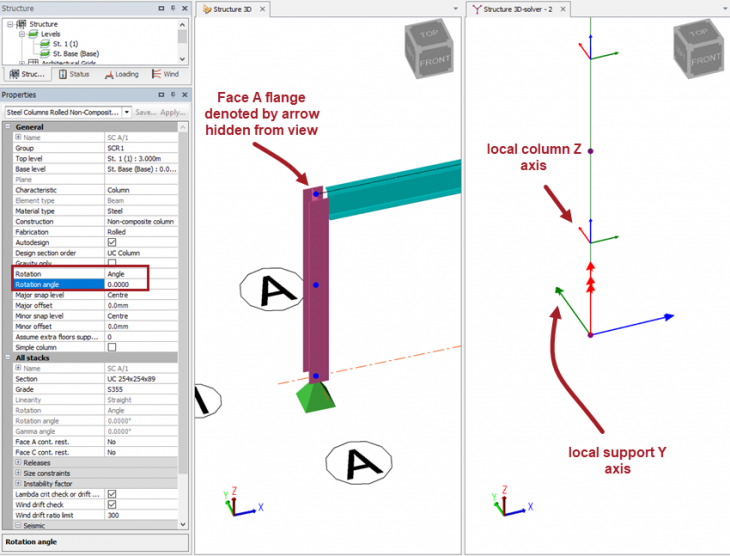
Rotation of column 90 deg
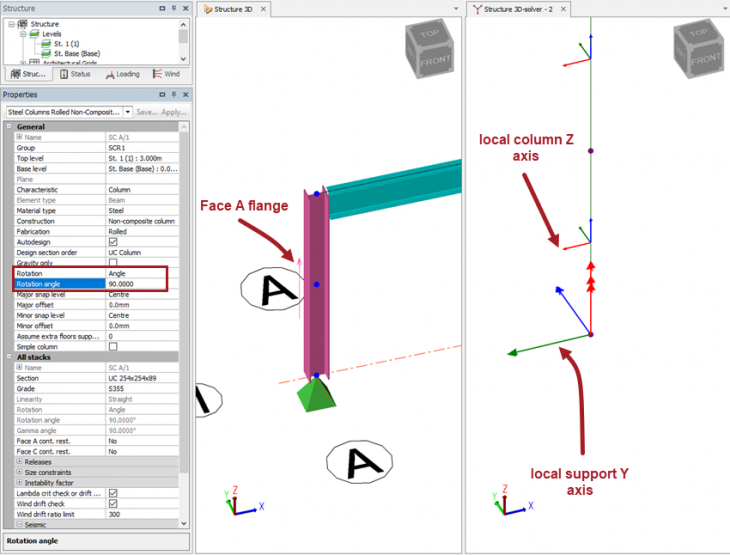
Rotation of column 180 deg
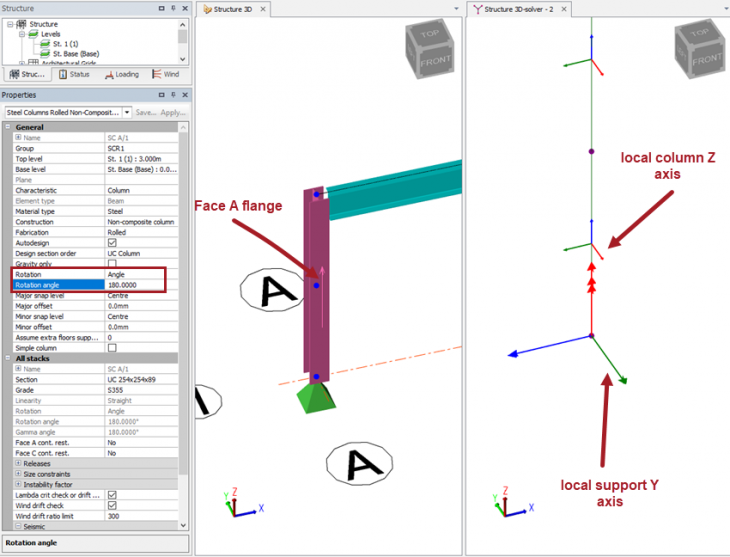
Rotation of column 270 deg
Findings
Clearly the rotation of the column can be any value between 0 and <360 degrees. By inspection of the various angles in the preceding screenshots we can determine that the local column z-axis (red) is always aligned to Face A of the column. Furthermore, the local support y-axis is also always aligned with Face A.
To summarize then:
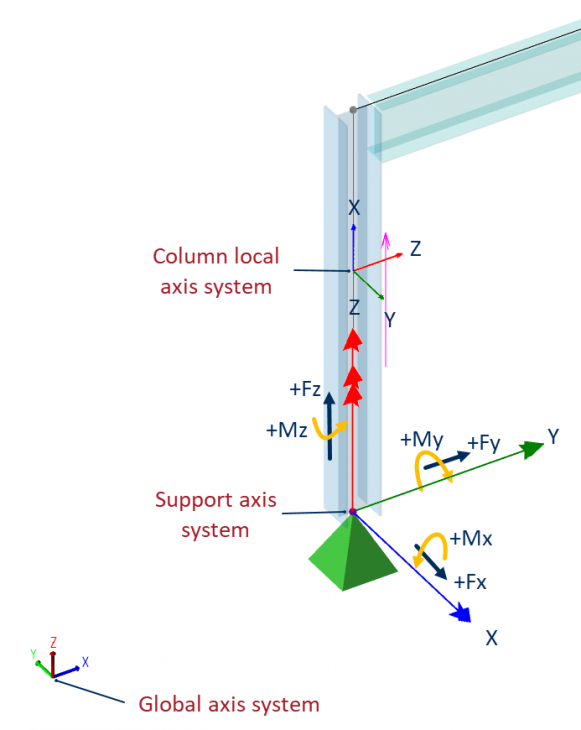
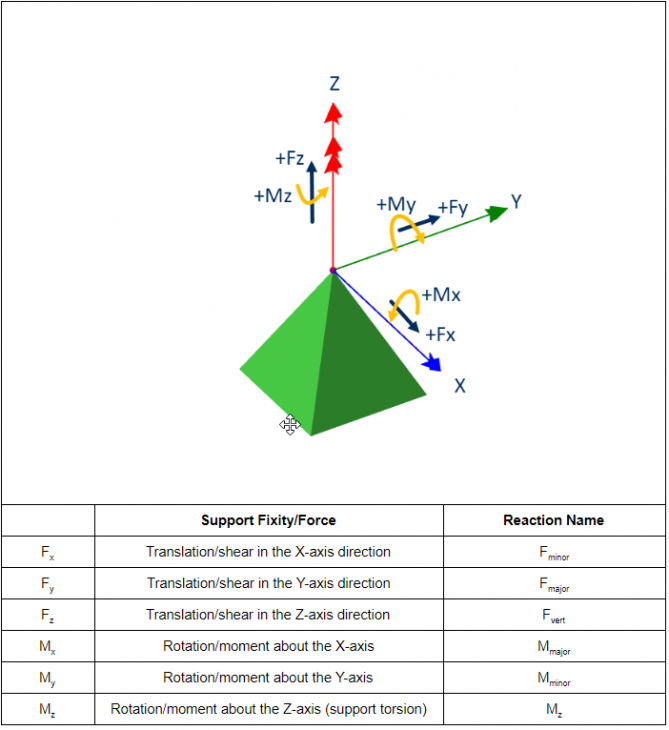
The support angle is fixed to that of the column and cannot be edited directly. Thus, if the column rotation is changed the support automatically follows this. See the diagram below which shows a vertical column and the +ve reaction forces. The column support y-axis is always aligned with the column local z-axis and the support z-axis is always aligned with the Global Z-axis. The support x-axis is orthogonal to these following the right hand rule (index finger along x-axis, thumb along y-axis). This results in the following convention of support fixities.
Fx: Translation in the column local y-axis (in both directions)
Fy: Translation in the column local z-axis (in both directions)
Fz: Translation in the Global Z-axis (vertical up/down)
Mx: Rotation about the Major axis
My: Rotation about the Minor axis
Mz: Rotation about the Global Z-axis (support torsion)
Now we understand this, we are able to confidently adjust the support fixities.
For completeness here is a table to explain the relationship between the Support axis system and those used for Reaction reports.
Taking the rotation of the column as 90 or 270 degrees so than it acts in the major axis for a globally applied X direction load, if we wish to apply a fixity to the column to resist this global X direction load then we must apply the fixity or spring about the (local) support x-axis (i.e. the Major Axis).
Taking the rotation of the column as 0 or 180 degrees so than it acts in the minor axis for a globally applied X direction load then if we wish to apply a fixity to the column to resist this global X direction load then we must apply the fixity or spring about the (local) support y-axis (i.e. the Minor axis).
Example
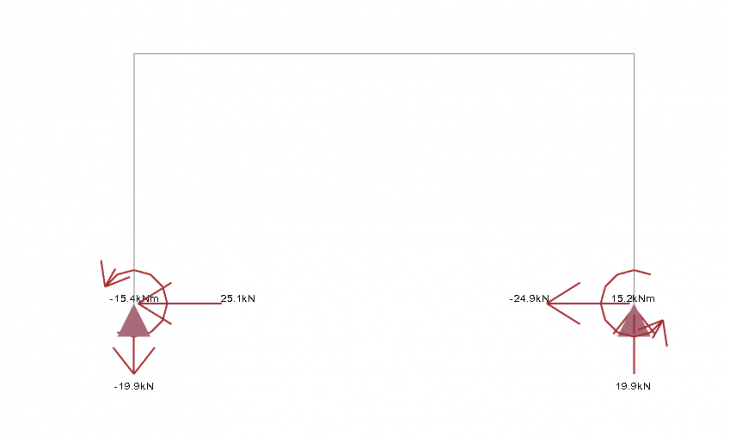
Let us reinforce this by way of a simple example using a moment goal post frame (beam and columns are fixed to allow moment transfer). Initially the supports are pinned. A fictitious horizontal load is applied to the top of the left hand column. The columns are oriented so that Face A flange is to the outside. This means that the left hand column rotation angle is 90 deg and the right hand column rotation angle is 270 deg. The local support axis is therefore different.
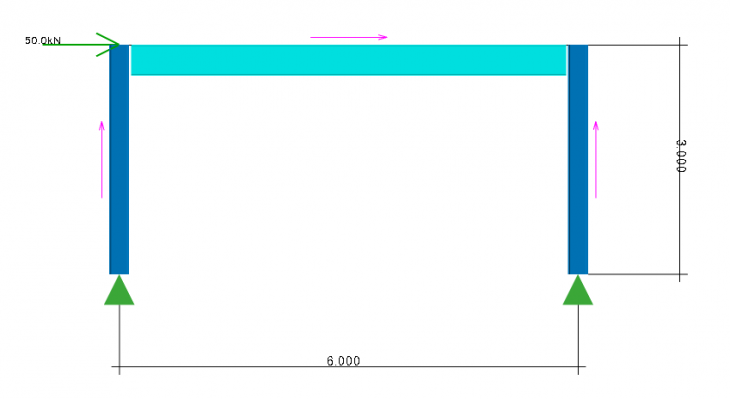
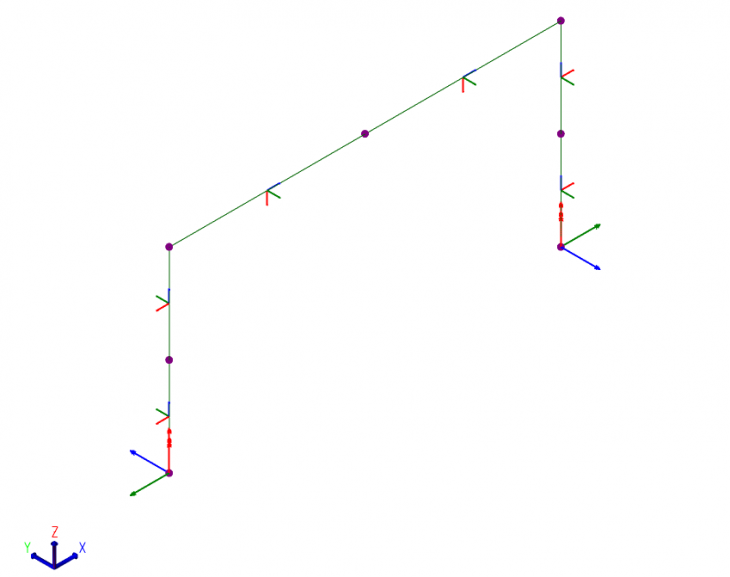
The analysis results for a pinned support
Deflection

Moment
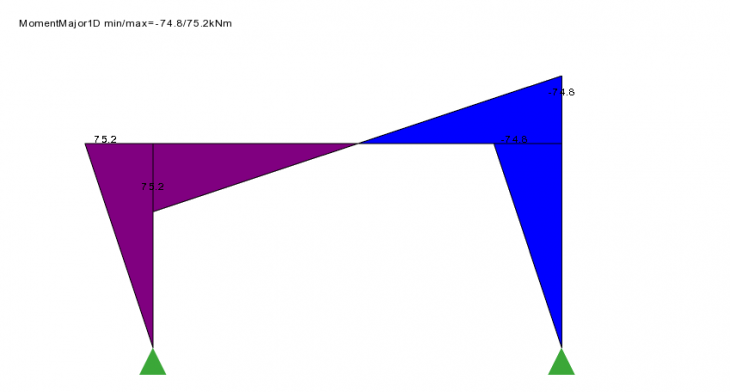
Shear
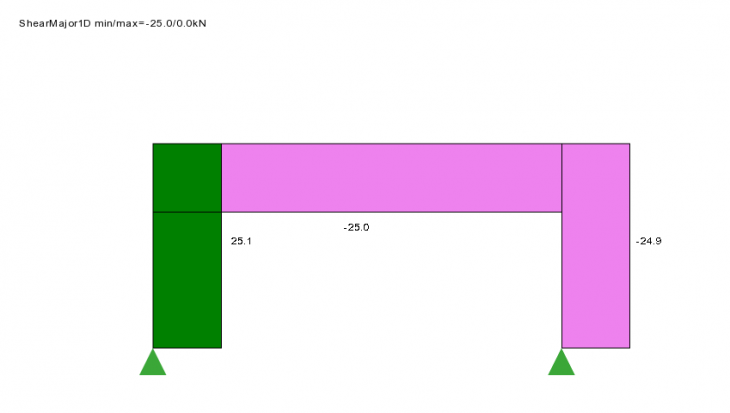
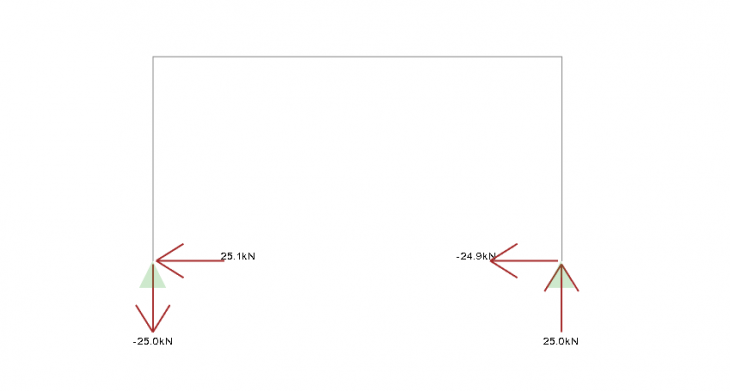
Reactions
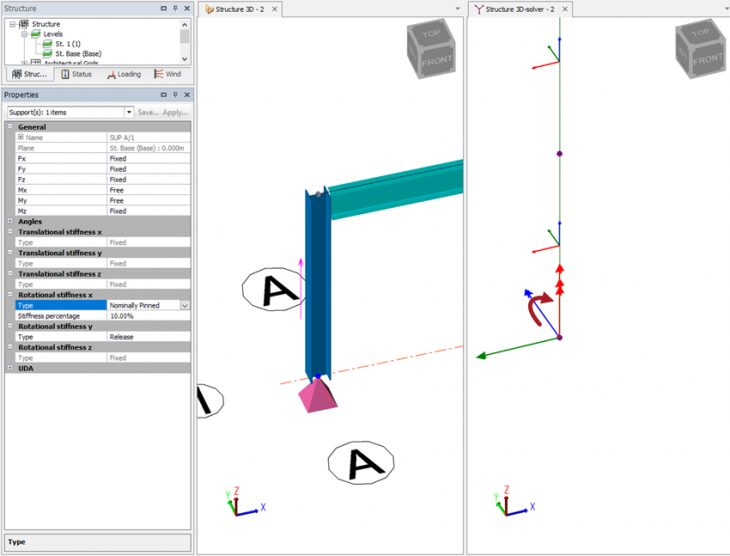
Now we wish to apply some rotational fixity to the supports. From the knowledge gained earlier this is to be applied to the local support x-axis (i.e. the major axis of the column)
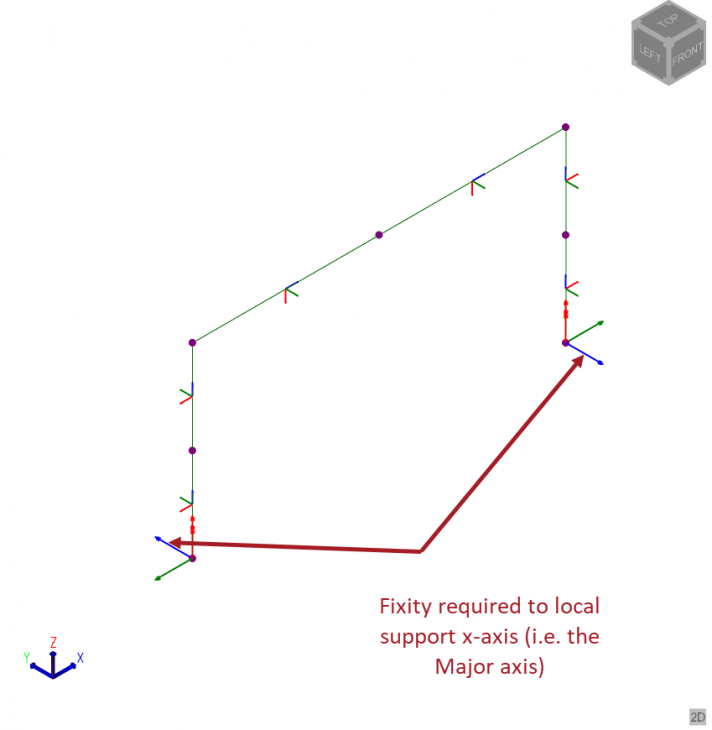
Select the support(s), we have selected both in this example since we wish to adjust the stiffness in the x-axis support direction for both.
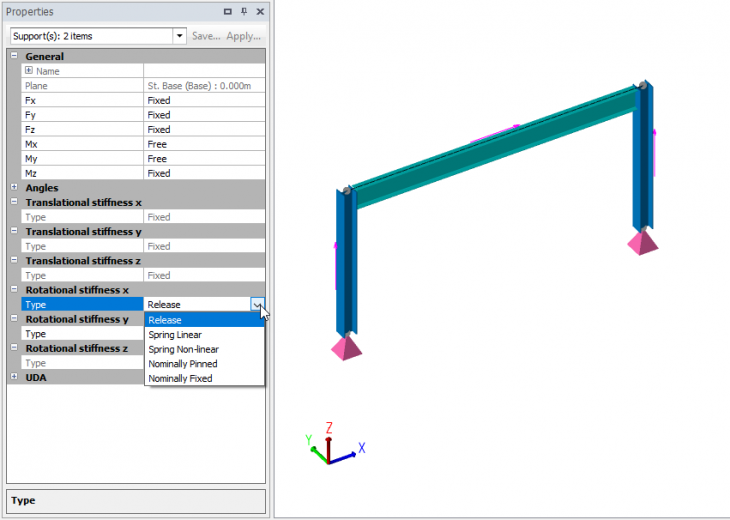
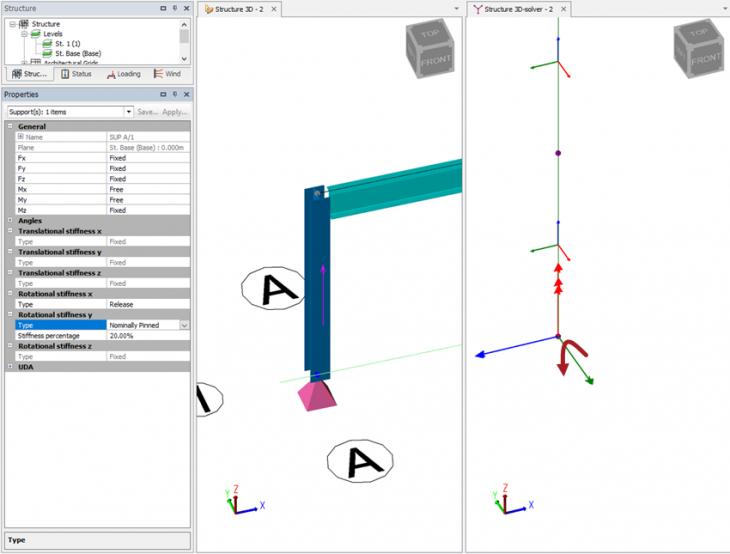
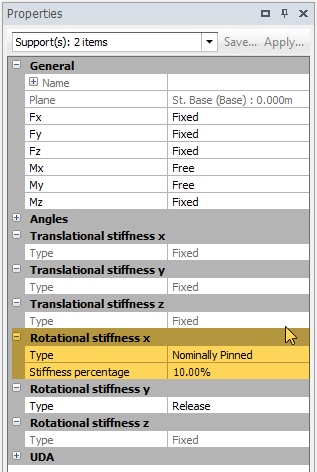
We will set as Nominally pinned, 10%.
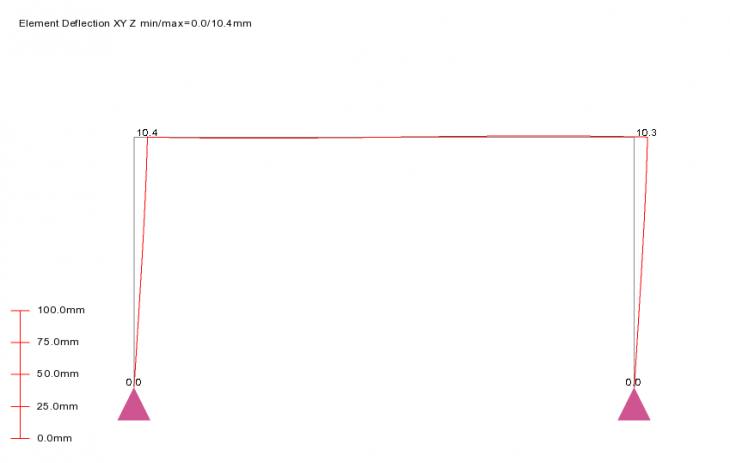
Running the analysis and reviewing the deflection diagram we can clearly see the reduction in deflection due to the stiffness assumed at the base support. 10.4mm (14mm without fixity)
Deflection
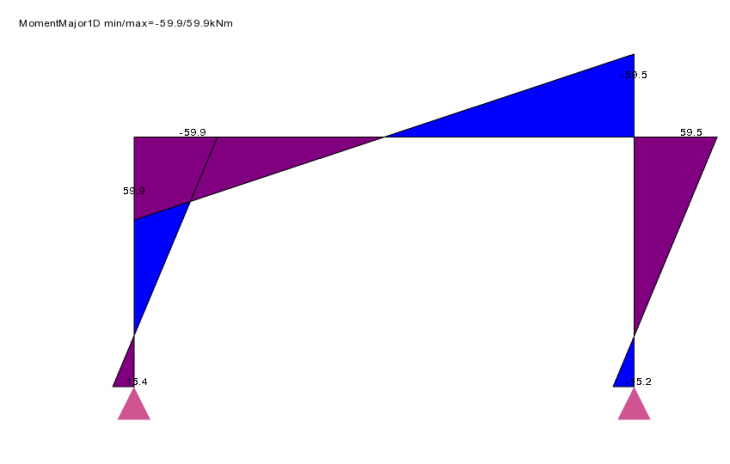
Moment
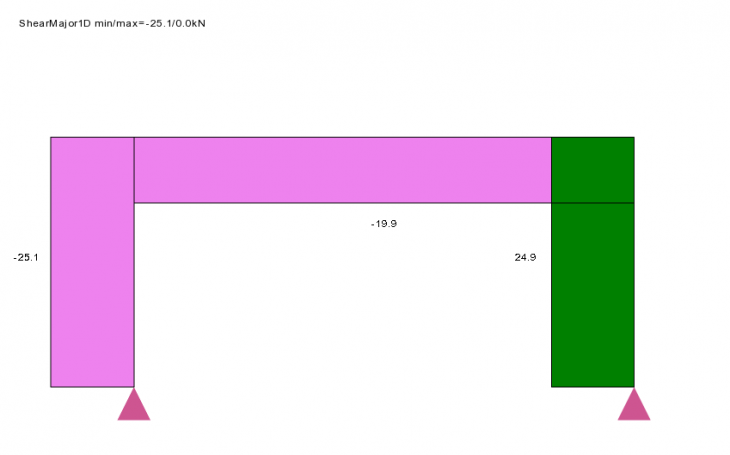
Shear
Reactions
We can now see a moment at the bases due to the rotational fixity.