How are the slab design moments determined using FE Analysis?
Question:
When looking at the design moment contours, I see they do not match the moments in their corresponding directions, why do the moments Mx and My and design moments Mdx and Mdy differ?
Answer:
Single Directional Moments
The output from the FE analysis of the FE shell mesh produces bending moments in two directions, x & y. These results are given in the forms listed below:
- Mx – moment acting on the x face (resulting from spanning in the x-direction)
- My – moment acting on the y face (resulting from spanning in the y-direction)
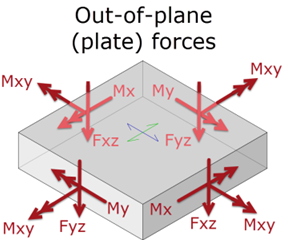
The diagrams were taken from the following support article, How do I interpret 2D Results (FE Contour Forces) and what are the Sign Conventions?
Directional Design Moments
The design moments separate the moments in each direction into the top and bottom surfaces - i.e. moments that cause tension on these surfaces, and also include a component of the twisting moment, Mxy, resulting in the design Wood Armer moments. This produces 4 design moment contours:
- Mdx,top
- Mdx,bottom
- Mdy,top
- Mdy,bottom
Reference can be made to R.H.Wood – The reinforcement of slabs in accordance with a pre-determined field of moments”, Concrete, February 1968 for these calculations.
Why are the Wood Armer moments required?
Twisting moments Mxy (or M12 in plate theory) are real forces which exist in panels following Plate Theory (for more on this see https://en.wikipedia.org/wiki/Plate_theory). Wood and Armer (see reference above) adjusted design moments is a method of accounting for the twisting effect which was developed by two professors initially used to consider twisting for skewed bridge decks. This sort of adjustment being the most common which has since been adopted into standard industry practice. Since twisting may be significant, clearly it is not logical to ignore the twisting moments in design. Using Wood Armer moments is the method adopted in Tekla Structural Designer for doing so.How are the design moments calculated?
This follows the same convention used in Tekla Structural Designer where a positive moment is one which produces tension on the Top surface . To calculate the top design moments upper and lower limits are required for each direction, in the calculations shown below, the limits in the x direction are taken as Mx1 and Mx2, similarly My1 and My2 in the y direction.Top Design Moments
Mx1 = Mx + | Mxy |My1 = My + | Mxy |
Mx2 = Mx + | ( Mxy2 / My ) |
My2 = My + | ( Mxy2 / Mx ) |
If both Mx1 and My1 are positive, then Mdx,top = Mx1 and Mdy,top = My1
If both Mx1 and My1 are negative, then Mdx,top and Mdy,top = 0 kNm/m
If Mx1 is negative and My1 is positive, then Mdx,top = 0 and Mdy,top = My1
If Mx1 is positive and My1 is negative, then Mdx,top = Mx1 and Mdy,top = 0
Mdx,top and Mdy,top are then used as the design moments in place of Mx, My and Mxy.
Bottom Design Moments
Mx1 = Mx - | Mxy |My1 = My - | Mxy |
Mx2 = Mx - | ( Mxy2 / My ) |
My2 = My - | ( Mxy2 / Mx ) |
If both Mx1 and My1 are positive, then Mdx,bot and Mdy,bot = 0
If both Mx1 and My1 are negative, then Mdx,bot = Mx1 and Mdy,bot = My1
If Mx1 is negative and My1 is positive, then Mdx,bot = Mx2 and Mdy,bot = 0
If Mx1 is positive and My1 is negative, then Mdx,bot = 0 and Mdy,bot = My2
Mdx,bot and Mdy,bot are then used as the design moments in place of Mx, My and Mxy.
Worked Example
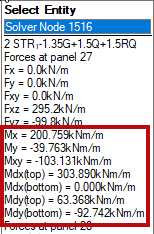
The example shown below shows an extreme example of how twisting moments can affect the overall slab design moments at a certain point. This example looks at a point where there is a change in slab depth where the twisting moments are high. In many cases, twisting will have little effect on the design moments.- Mx = 200.759
- My = -39.763
- Mxy = -103.131
Top Moments
Mx1 = 200.759 + 103.131 = 303.9My1 = -39.763 + 103.131 = 63.4
Both Mx1 and My1 are positive:
The top design moments are taken as:
Mdx,top = Mx1 = 303.89 kNm/mMdy,top = My1 = 63.37 kNm/m
Bottom Moments
Mx1 = 200.759 – 103.131 = 97.63My1 = 39.763 – 103.131 = -142.89
Where Mx1 and My1 have different signs and Mx1 is positive, we know that Mdx,bot = 0. My2 is required to calculate the bottom design moment in the y direction.
My2 = -39.763 – 103.1312/200.759 = -92.75
The bottom design moments are taken as:
Mdx,bot = 0 kNm/mMdy,bot = |My2| = 92.75 kNm/m